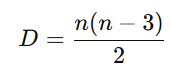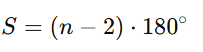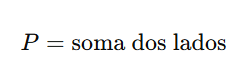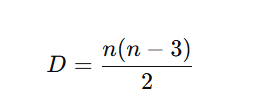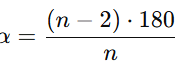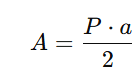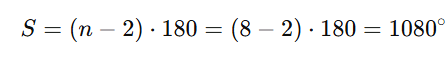Polígonos: conceitos, tipos, propriedades e cálculos

Os polígonos são figuras geométricas planas formadas por segmentos de reta que se encontram em pontos chamados vértices. Eles são essenciais na geometria plana e aparecem em diversas áreas, da matemática à engenharia e arquitetura.

O estudo de polígonos envolve:

• Classificação dos polígonos 
• Reconhecimento de lados, vértices e ângulos 
• Identificação de polígonos regulares e irregulares 
• Cálculo de perímetro e área 

Entre os polígonos mais comuns estão triângulos, quadriláteros, pentágonos, hexágonos, entre outros.

Como classificar um polígono?

A classificação dos polígonos é feita segundo dois critérios principais:

• Número de lados: 
  • Triângulo: 3 lados 
  • Quadrilátero: 4 lados 
  • Pentágono: 5 lados 
  • Hexágono: 6 lados 
  • Heptágono: 7 lados 
  • Octógono: 8 lados 
  • Eneágono: 9 lados 
  • Decágono: 10 lados 
• Regularidade: 
  • Polígonos regulares: todos os lados e ângulos iguais 
  • Polígonos irregulares: lados e ângulos diferentes 

Quais são os tipos de polígonos?

Triângulos

• Equilátero: 3 lados iguais 
• Isósceles: 2 lados iguais 
• Escaleno: todos os lados diferentes 

Quadriláteros

• Quadrado: 4 lados iguais, ângulos retos 
• Retângulo: lados opostos iguais, ângulos retos 
• Losango: 4 lados iguais, ângulos opostos iguais 
• Trapézio: apenas um par de lados paralelos 

Polígonos com 5 ou mais lados

• Pentágono: 5 lados 
• Hexágono: 6 lados 
• Heptágono: 7 lados 
• Octógono: 8 lados 
• Todos podem ser regulares ou irregulares 

Quais são os elementos de um polígono?

Todo polígono possui:

• Lados: segmentos de reta que formam a figura 
• Vértices: pontos de encontro dos lados 
• Ângulos internos: formados entre dois lados adjacentes 
• Diagonais: segmentos que ligam vértices não consecutivos 

Fórmulas importantes:

• Número de diagonais:

• Soma dos ângulos internos:
  

Propriedades dos polígonos

• Polígonos convexos: todos os ângulos internos menores que 180° 
• Polígonos côncavos: pelo menos um ângulo interno maior que 180° 
• Polígonos regulares: lados e ângulos iguais; podem ser inscritos em uma circunferência 
• Perímetro: soma de todos os lados do polígono 

O que é um polígono regular?

Um polígono regular possui:

• Todos os lados iguais 
• Todos os ângulos iguais 
• Simetria perfeita 

Exemplos: quadrado, hexágono regular, pentágono regular

Fórmula do ângulo interno de um polígono regular:

α=(n−2)⋅180n\alpha = \frac{(n-2) \cdot 180}{n}α=n(n−2)⋅180​

Como calcular a área de um polígono?

O cálculo da área de um polígono depende do tipo da figura e das suas dimensões.

• Triângulo: Para calcular a área de um triângulo, multiplica-se a medida da base pela altura e divide-se o resultado por dois. A base é qualquer um dos lados escolhidos como referência, e a altura é a distância perpendicular da base até o vértice oposto. 
• Quadrado: No quadrado, basta multiplicar o comprimento de um dos lados por ele mesmo, já que todos os lados têm a mesma medida. 
• Retângulo: A área de um retângulo é obtida multiplicando-se a medida da base pela altura. A base e a altura são os lados que se encontram formando ângulo reto. 
• Polígono regular (com n lados): Para um polígono regular, que possui todos os lados e ângulos iguais, a área pode ser encontrada multiplicando-se o perímetro total pelo apótema, que é a distância do centro até o meio de um lado, e dividindo o resultado pela metade. 

Tabela resumida dos polígonos até decágono

Fórmulas resumidas para polígonos

• Perímetro: 

• Número de diagonais: 

• Soma dos ângulos internos: 

• Ângulo interno de polígono regular: 

​

• Área do polígono regular: 

Exercícios de fixação

Calcule a soma dos ângulos internos de um octógono.

Resposta:

Comentário:
Para calcular a soma dos ângulos internos de qualquer polígono, usamos a regra que considera que um polígono de n lados pode ser dividido em triângulos, cada um com soma de ângulos igual a 180°. A fórmula S = (n-2) × 180° reflete essa ideia: subtraímos 2 do número de lados porque um triângulo é a menor figura possível para formar polígonos.

No caso do octógono, que tem 8 lados, a subtração de 2 nos dá 6 triângulos imaginários dentro do polígono. Multiplicando 6 por 180°, obtemos 1080°, que é a soma de todos os ângulos internos.

Isso significa que, se quisermos saber o valor de cada ângulo em um octógono regular (onde todos os ângulos são iguais), basta dividir 1080° por 8, resultando em 135° por ângulo.